とします。一般の n1th 近似値は nth 近似値より n a n)/2 により求めます。この初期値(第0近似値)の選び方により、収束の早さは異なりますが、この近似法はかなり収束が早く、実用上は5回ぐらいで十分な値が得られます。このように, 値を持っていたとしても他の数と比べると十分に小さいならば無視する操作 を近似という 高校物理で頻出の 近似公式 としては次のようなものがある真 の 値 に 近 い値をいい、測定や近似計算によって得られる。 たとえば15℃の空気中の音の速さの近似値は毎秒340メートル、分数1/3の近似値は033、 円周率 の近似値は314などである。

中学数学3年 平方根とその近似値 大小 有理数と無理数 受験の月
近似値とは ルート
近似値とは ルート-高速根号計算 (fast sqrt algorithm) 概要 C言語のsqrt (float)より精度は若干劣るものの,2倍以上速いsqrtのalgorithm. ググって見つけた物が,非常に面白かったのでまとめておく. 精度より速度が求められる場面で活躍する(シェーダとか). 精度はあまりで無理数で使う近似値とは、ルートのついた循環しない無限小数に区切りをつけてあつかう小数のことです。 13 近似と極限 上の2つの例の, 大 日本 住友 製薬 自殺




中学数学 平方根 のコツ 平方根の近似値 式の値
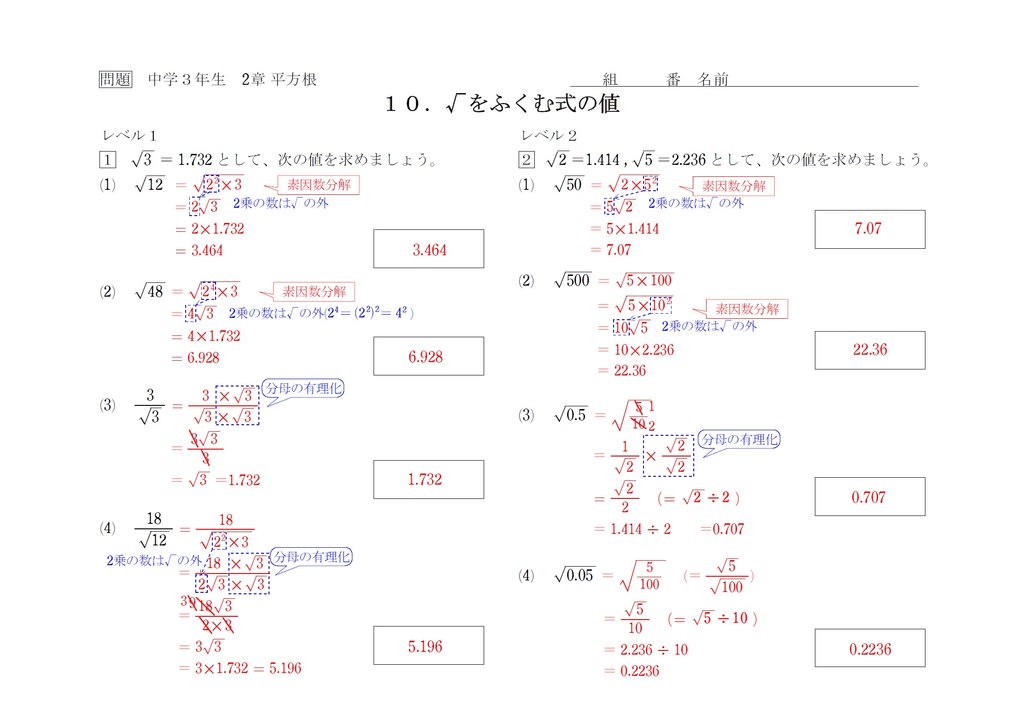
実際のルート10の値は「」という値なので、先ほどの操作で求められた近似値、つまり ルート10 ≒ ab = は小数点第3位まで正確連分数展開の求め方 α の連分数展開を求めたい (1) α を整数部分a0 と小数部分b0 に分ける α = a0 b0 (0 < b0 < 1) (2) α1 = 1 b0 とおいて α1 を整数部分a1 と小数部分b1 に分ける α1 = a1 b1 (0 < b1 < 1) このとき α = a0 b0 = a0 1 α1 = a0 1 a1 b1 (3) α2 = 1 b1 とおいて α2 を整数部分a2 と小数部分b2 に分ける (4 平方根(ルート)の近似値の求め方 √2≒141 というのは聞いたことがありますか? 平方根を、近い大きさの数である「近似値」で表せ、という問題はよく出題されます。ここではこの、「平方根の近似値」について説明します。 覚えるべき近似値
02 ルートの近似値 続いて次の値の近似値を求めてみましょう! まず次のように変形します: すると x = 7/121 = を微小量 x とみなして、先ほど求めた近似式を用いることができます: 右辺を計算することで √128 の近似値が求まりました! ニュートン法とは、f (x)=0になるようなxを求めるアルゴリズムの1つで、方程式の解を近似的に求めることができる方法です。 ニュートン法を用いると、√2の値やsin (x)=05になるようなxの値など近似的に求めることができます ルート19万円ほしい っていわれてもピンとこないよね??笑 高いのか低いのか検討もつかん。 今日はそんな事態に備えて、 平方根のだいたいの値の求め方を勉強していこう。 この「だいたいの値」のことを、 数学では「 近似値 」とよんでいるんだ。 3
これは「本当は有理数なのだけど分母が分からない」という近似値が与えられたときに、 分母を推定するための強力な武器となります。 例えば 近似値: x = 連分数展開: 0, 1, 1, 1, 95, 1, 1, 1, , 1, 1, 2, 1, 21, 3, 1,関数の近似とTaylor 展開 微分係数と接線の方程式 実数x の関数f(x) のx0 における微分係数f′(x 0) の定義は次の様に書き換えることが出来る。 lim x→x0 f(x)−f(x0) x−x0 −f′(x 0) = 0 つまりf(x) = f(x0)f′(x0)(x−x0)R(x) とおくと lim x→x0 R(x) x−x0 = 0 このことは を の近くで一次関数 で近似す小数だと近似値の右に次々に数字を付け加えること でより良い近似値が得られるのに,分数ではそうはいかないではないか,というように。 しかしながら本稿では,1と2の間をできるだけ粗く区切って,それでもよい近似値を得るというこ とを考えましょう。




データの分析 無理数の近似値の求め方 数学 定期テスト対策サイト




ルート2を連分数の極限として求めようとしたら行列が出てきた 前編 しいたげられたしいたけ
平方根・累乗根 110 /件 表示件数 5 10 30 50 100 0 1 0116 歳代 / 高校・専門・大学生・大学院生 / 役に立った / 使用目的 e=11程度のRSAを復号するため 2 1442 30歳代 / 主婦 / 非常に役に立った / 使用目的近似値を求められるんです。 以下で解説していきますね。 まずは準備体操を! 平方根の 「近似値」 の問題は、 √2 や √ の使い方が 基本になるのですが、 そうした基本の話(練習の第一歩)は、 こちらのページ で解説しています。 かなり大事な値がはっきりと分かるので(たとえば93mmとしよう)、そ れを満足するように、つまり(X,Y)=(0,93)を通るようにフ ィットする方が正確である。このような条件付きのフィット を行うには、図2のダイアログ・ボックスで「通過点」をチェ




近似値と有効数字の求め方とは どちらも情報の 度が大事 遊ぶ数学




中3数学 平方根の近似値の問題です Clear
ルート23の場合 23 のように、簡単な 素数 のかけ算に直せない値の平方根の場合は、以下の手順を踏みます。 Step① 2 乗した値が 23 以下となる最大の整数 n を考える ( n = 4) Step② n を筆算の上に1個、左に2個並べて書く(2個目に+をつける) Step③ 23 から nStart studying ルート(√) 16までの近似値(小数第4位以下切り捨て) 数学 平方根 Learn vocabulary, terms, and more with flashcards, games, and other study tools ルート(根号)の外し方がイマイチわからん・・・! こんにちは!この記事をかいてるKenだよ。ウェイトは重いね。 平方根の問題はたくさん、ある。 ルートの計算問題とか、 平方根の大小をくらべる問題とか、ルートの近似値を求める問題とかね。




高校数学 近似値 平方根 円周率 常用対数 自然対数の底 のゴロ合わせ 受験の月




中学数学 平方根 整数になる自然数n の簡単なやり方 丁寧な解説 スタディーランナップ
タを利用して、 の近似値を求めた。それは、次のような漸化式で定まるものである。 この漸化式は、次のような ニュートン・ラフソン法 により、簡単に求められる。コラム 「ルートの近似 但し、調整項はその絶対値が最小のものとする。 答. 24 = 49 2 ・・・② 24 = 50 2 1, α 2, を次のように定義します。要するに、1 と 2 の 算術調和平均 が 2 の平方根だ、という当たり前のことを仰っているのですね。 なお、2 の平方根の近似分数を得るには、 連分数 を用いる方がずっと効率が良いことが知られています。 ところで、 Helpノートページ#記事ページ に




平方根の問題の解き方 6パターン 数学fun




裏技公開 11のような平方根を速く求める方法 連分数使います Cupuasu クプアス
平方根 (ルート) を覚えることをやめました。 どうも,ユキです。 平方根を自分で導くことが出来れば,覚える必要はありませんよね。 ということで,今回の話は,連分数を使って, 平方根の近似値を出す裏技 を公開します。P値(Prob>ChiSq) 検定の p 値。この p 値は、自由度をXの水準数から1を引いた値としたカイ2乗分布に基づいています。 二標本 正確検定 データがまばらであったり、歪んでいたり、同順位が多い場合は、正確検定のほうが、漸近的な近似検定よりも適しているルート2を求める $141$ まで。次の $1414$ なんて電卓がないとやる気が起こりません。本当に $\sqrt{2}$ の値を深く求めたいのであれば,やり方を変えた方がよさそうです。




平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ



中学数学 平方根
Review (Approximate calculation by tangent line) Example sin59 の近似値を1 次近似で求めてみる. y = sin x のx = π/3 における接線l は l y = 1 2 x √ 3 2 − π 6 なので,x ≒ π/3 ならば sin x ≒ 1 2 x √ 3 2 − π 6 が成り立つ.そこで,x = 59 = 59π/180 とすれば sin59 ≒ √




中学数学 平方根 のコツ 平方根の近似値 式の値




中学数学 平方根 のコツ 平方根の近似値 式の値




ルート2 ルート3 ルート5の覚え方など 高校数学の美しい物語




ルートの近似値の求め方 不等式を使って大小比較 趣味の大学数学




中3 ルートの近似値の求め方をイチから解説 Youtube




中3数学 平方根 18 中学数学高校数学個別指導in山形市 数専ゼミ




無料 中3数学 発展 応用問題 問題プリント 314 平方根6 いろいろな計算1



1




中1数学 近似値と誤差のポイントと練習問題 中学生勉強サイトあかね先生
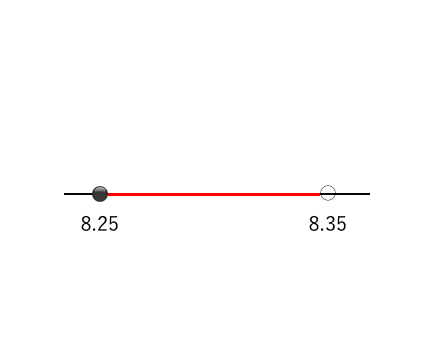



近似値の問題 苦手な数学を簡単に




ルート2 ルート3 ルート5の覚え方など 高校数学の美しい物語



平方根の近似値 勉強ナビゲーター




中3数学 平方根の近似値の問題です Clear



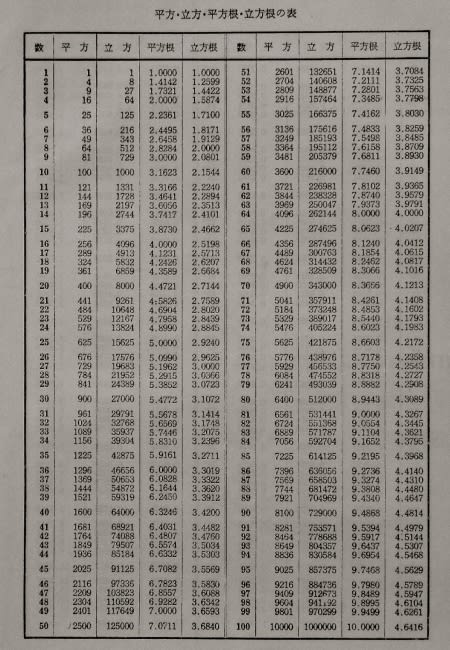
中3数学です 次の数の近似値を 平方根表を使って 小数第3位ま Yahoo 知恵袋




ルート3の近似値の求め方4パターン 数学の星



3




平方根で近似値の応用問題です はどうやって解きますか Clear




平方根近似値早技 Cupuasu クプアス



1




6 の正しい近似値を教えてください 左がネット 右が教科書 です Clear



平方根まとめ




中1 数学 中1 近似値 Youtube




裏技公開 11のような平方根を速く求める方法 連分数使います Cupuasu クプアス



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス




平方根のおよその値の求め方とその利用 わかるようになる高校数学



平方根の計算方法



関数電卓でルートxの近似値を出してくれる方法を教えてください ル Yahoo 知恵袋



Www1 Iwate School Jp Action Common Download Main Upload Id 1384




近似計算 高校物理をあきらめる前に 高校物理をあきらめる前に




中学校数学 3年生 数量 平方根 Wikibooks




平方根 近似値を求める 苦手な数学を簡単に




中3 数学 平方根6 ルートの近似値 4分 Youtube




ルート2を連分数の極限として求めようとしたら行列が出てきた 前編 しいたげられたしいたけ




平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ



中3 根号の近似値 の教え方 塾講師 数学マンは踊る
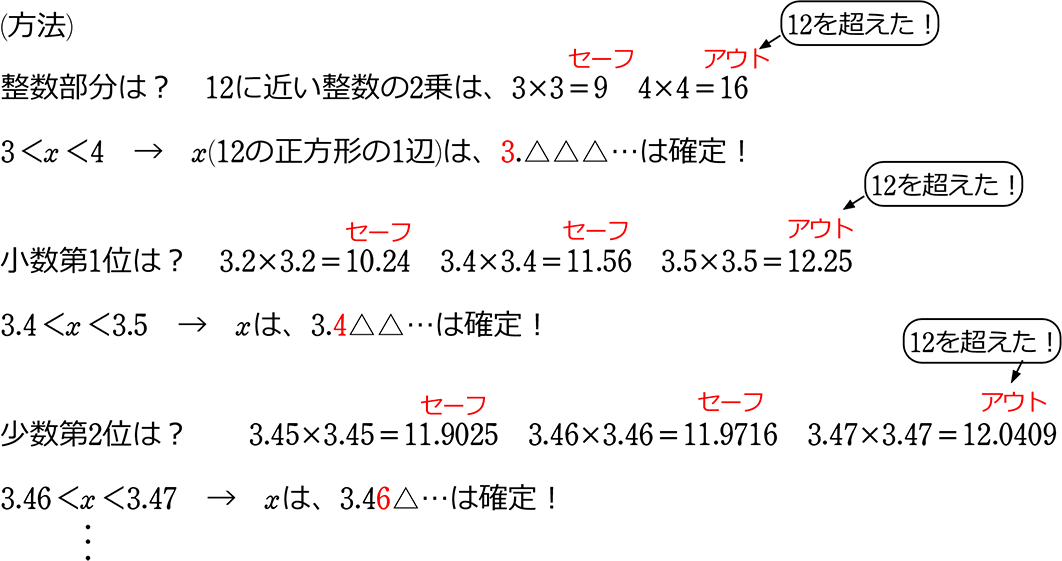



中学数学 平方根




平方根とは コトバンク
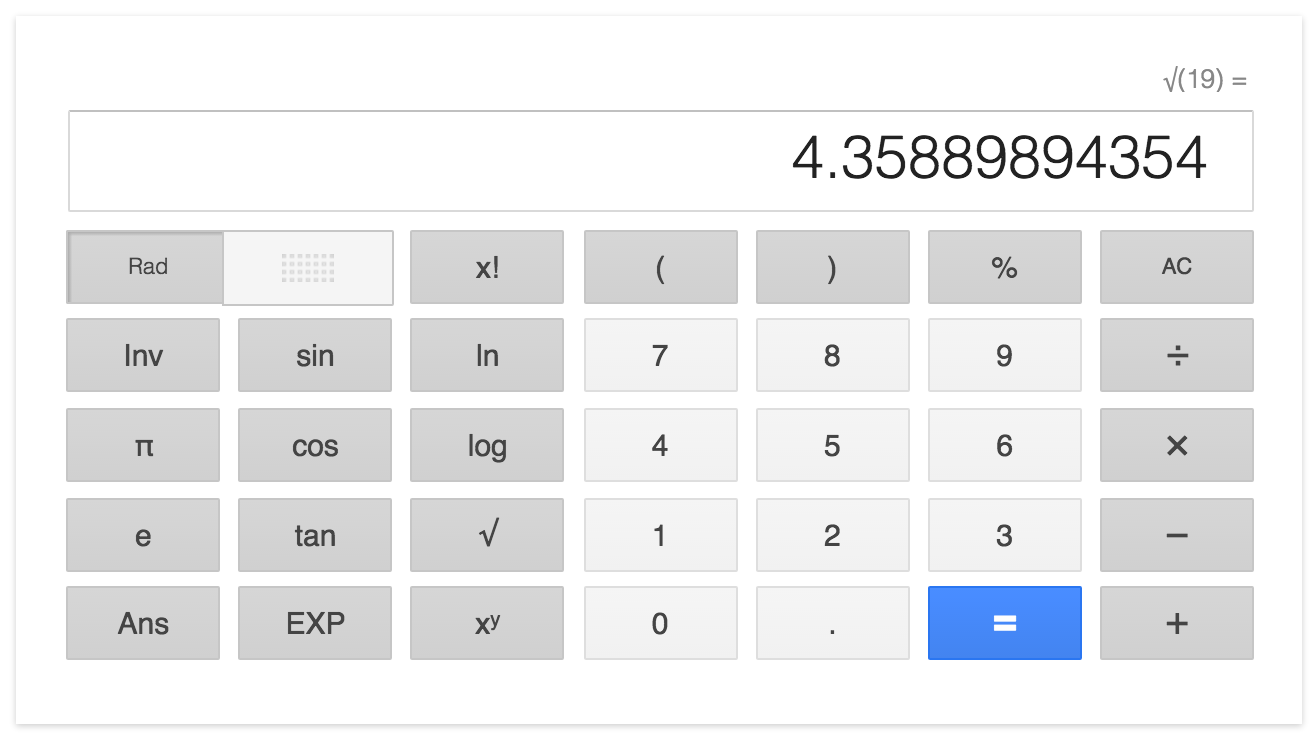



中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく




画像 ルート 展開 近似 ハイキュー ネタバレ




高校数学 近似値 平方根 円周率 常用対数 自然対数の底 のゴロ合わせ 受験の月




2の平方根 Wikipedia



平方根の手計算による解法 タックの庭仕事 黄昏人生残日録




中3 数学 無料学習プリント教材




数学 近似式まとめ 各種公式 求め方 理系ラボ




ルートの近似値の求め方 中3数学 Youtube



数 近似値 近似式 数学のコツ




平方根はこれで完璧 平方根の定義からルートの計算 近似値の問題の解き方まで




6 の正しい近似値を教えてください 左がネット 右が教科書 です Clear



平方根の近似値 この問題の意味が分かりません そもそも数字の並び Yahoo 知恵袋




中3数学 平方根 ルートの値を語呂合わせ 覚え方まとめ 数スタ




ニュートン法によってルート 円周率の近似値を求めてみよう 趣味の大学数学




平方根の近似値 無料で使える中学学習プリント



中3 平方根10 近似値 中学数学の勉強に




中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく




ルート3の近似値 よし坊のブログ




平方根 ルートの計算



平方根の近似値を求めるにはどんな考え方をするの 語呂合わせを使った覚え方は さびねこ中学校




ニュートン法の例題 ルート3の近似値を与える方法 理数アラカルト
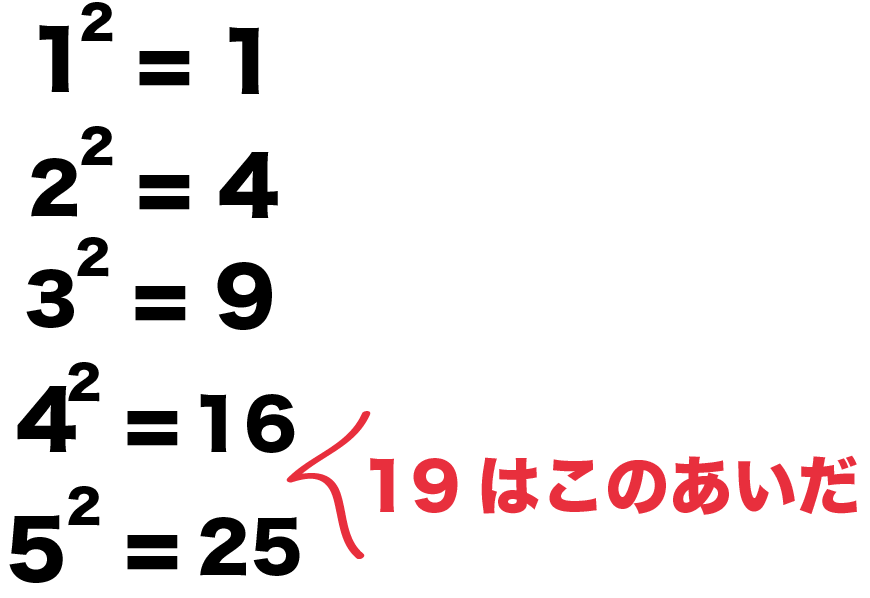



中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく




ルート 16までの近似値 小数第4位以下切り捨て 数学 平方根 Flashcards Quizlet




中学校数学 3年生 数量 平方根 Wikibooks




中学数学3年 平方根とその近似値 大小 有理数と無理数 受験の月




平方根の活用 式の値と近似値の求め方 教遊者
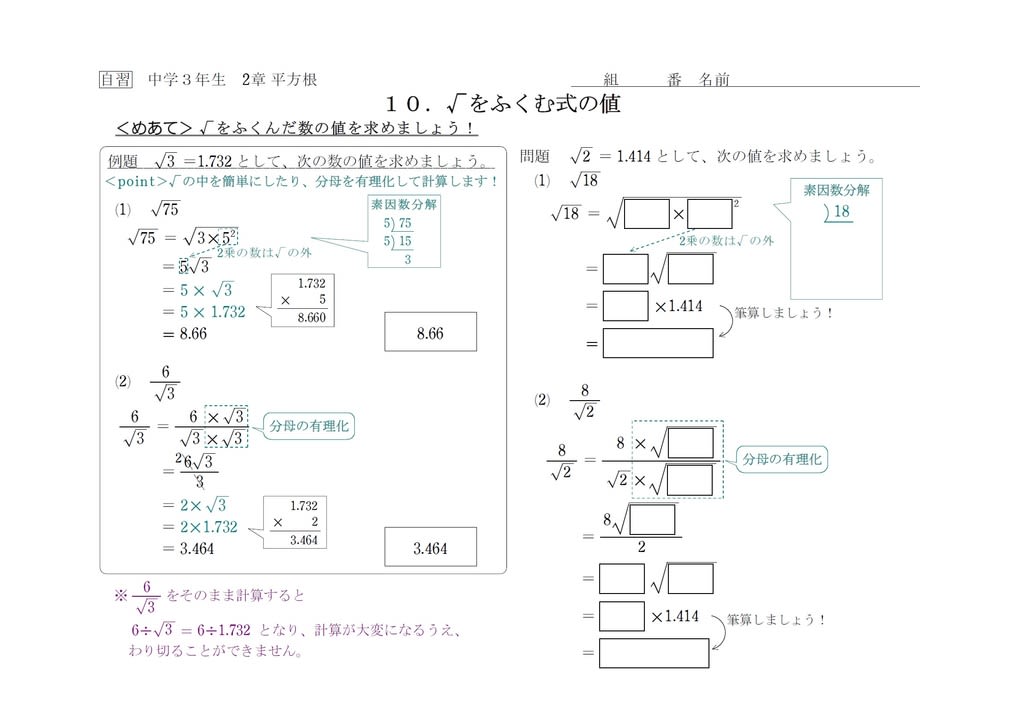



中3自習 平方根5 近似値 中学数学の勉強に




ルートの近似値を計算する素朴な方法とコツ 高校数学の美しい物語




勝手に北辰テスト対策 数学 平方根 蒼進塾 そうしんじゅく さいたま市 真剣に努力する姿勢を育む
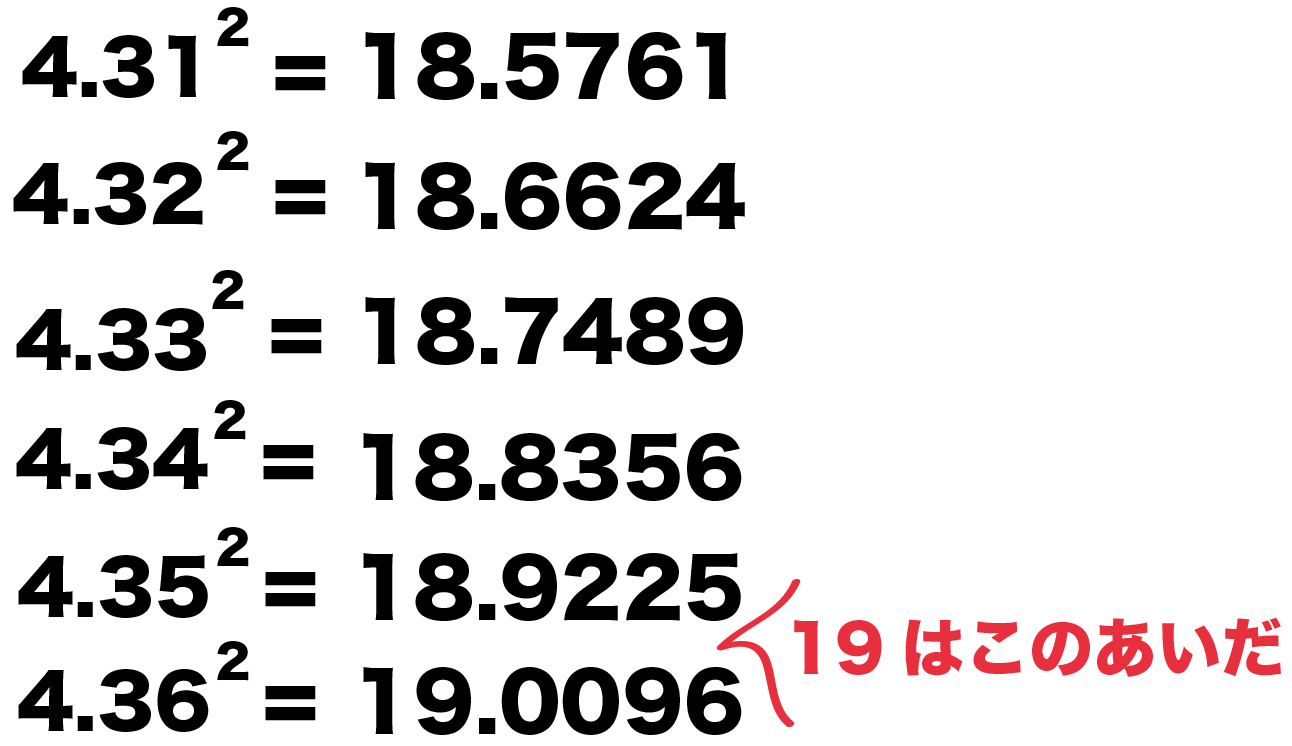



中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく



Python Tkinterで平方根の近似解を求めるguiツール G6no3 Blog




平方根 式の値 求め方はどうやる 問題を使って徹底解説 数スタ



三石 数学塾 ルート2を求める その4




平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ



第2章10平方根 平方根の近似値 ニュージーランド短期留学ダイアリー




中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく



しょうちゃん 公式ブログ 開平法 ルートの近似値の求め方 Powered By Line




中3数学 平方根の近似値 映像授業のtry It トライイット



3 732 30 477とするとき 次の近似値を求め Yahoo 知恵袋




中学数学 3分でわかる 平方根の近似値の求め方 Qikeru 学びを楽しくわかりやすく




ルート5ほかの近似値 三平方の定理 よし坊のブログ



中1です この近似値を教えて下さい 塾には行っていないので自分で一時間 Yahoo 知恵袋



平方根とは 計算方法や求め方 近似値の覚え方 利用問題 受験辞典



ルートを開こう




中3数学 平方根の近似値 Youtube
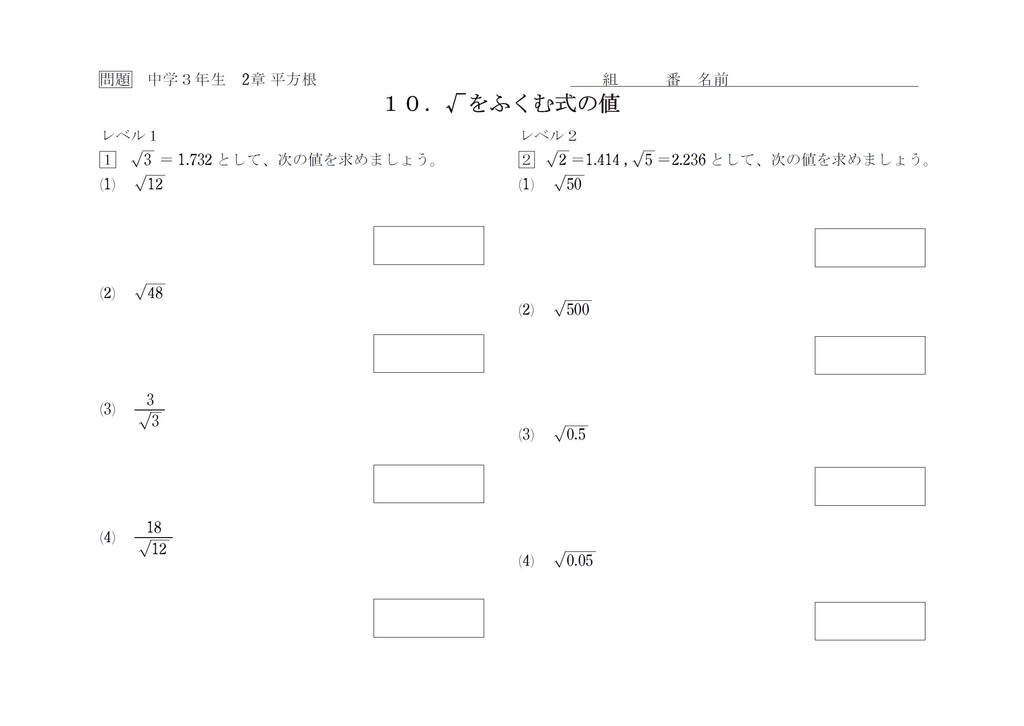



中3 平方根10 近似値 中学数学の勉強に




ルート3の近似値の求め方4パターン 数学の星




平方根 近似値を求める 苦手な数学を簡単に




Kio Miw على تويتر 以下のような技もあります 高精度のpi Pi Ent E の近似値 E Ent ルート2 Root2 Ent ルート3




計算機プログラムの構造と解釈 第二版




ルート2の近似値を知る その1 よし坊のブログ



電卓でルート 平方根 を計算する方法




ルート3の近似値の求め方4パターン 数学の星




平方根の近似値を語呂合わせで覚える わさん先生のうわごと




平方根の近似値 無料で使える中学学習プリント



H Kinji



1



0 件のコメント:
コメントを投稿